本节将在 MATLAB 环境下介绍如何实施层次聚类(Hierarchical Clustering),并重点讲解其树状图(dendrogram)结构的解读方法,以及多尺度分群的实际应用策略。
4. Part II – 层次聚类:树状图构建与多尺度结构识别
层次聚类通过计算样本之间的成对距离,并按照某种“合并代价最小”原则,逐步将样本两两合并为更大规模的簇,最终形成一棵嵌套型的聚类树(dendrogram)。它与 K‑Means 等划分式方法的最大区别在于:不需要预设簇数 KK,而是提供了完整的多尺度结构信息,研究者可根据具体问题选择合适的聚类层级。
4.1 算法调用与树状图构建
① 计算样本之间的距离矩阵
% 使用欧氏距离计算距离矩阵
D = pdist(X, 'euclidean');X 为预处理后的样本特征矩阵,pdist 返回上三角压缩形式的距离向量。
② 构建层次聚类树(linkage)
% 构建linkage矩阵,使用Ward方法(最小化方差增量)
Z = linkage(D, 'ward');ward方法倾向于生成方差最小、大小相对均衡的簇;- 其他可选方法包括
average(UPGMA)、complete、single,分别反映不同的簇间距离定义方式。
③ 绘制树状图(dendrogram)
figure;
dendrogram(Z, 0); % 第二参数设为0表示完整显示所有样本
title('层次聚类树状图(完整)');
xlabel('样本编号');
ylabel('合并距离(Euclidean)');如样本数较多,可使用截断模式仅展示聚合结果:
figure;
dendrogram(Z, 30, 'ColorThreshold', 'default');
title('层次聚类树状图(截断显示前30个合并节点)');注:Y轴越高表示簇间差异越大;水平切线可用作划分簇的门槛。
4.2 根据树状图进行簇划分
% 指定截断簇数(如3簇)
idx_hc = cluster(Z, 'maxclust', 3);也可以指定合并距离阈值:
% 指定合并距离阈值进行聚类
idx_hc2 = cluster(Z, 'cutoff', 6, 'criterion', 'distance');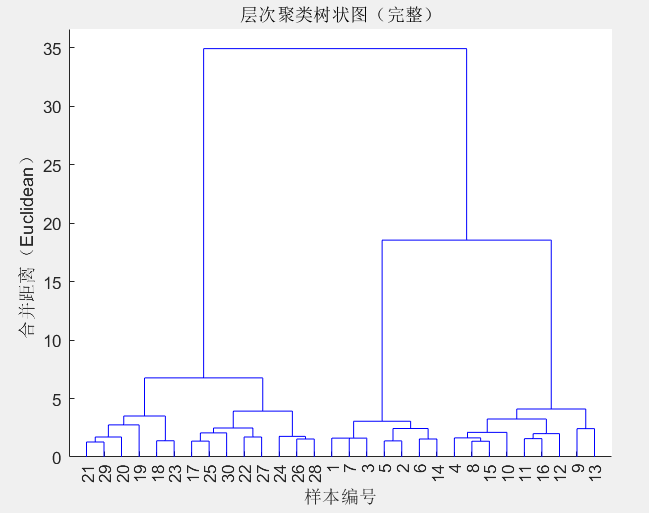
4.3 结果可视化与对比
可与 K-Means 结果对照观察:
% 主成分空间中可视化层次聚类结果
[~, score] = pca(X);
figure;
gscatter(score(:,1), score(:,2), idx_hc, 'rgb', 'o', 6);
xlabel('PC1'); ylabel('PC2');
title('层次聚类结果(投影至前两主成分)');
grid on;4.4 不同方法的聚类稳定性对比
% 对比K-Means与层次聚类的一致性(如ARI)
% 此处需使用TrueLabel作为参考(若有)
% 举例:使用adjustedRandIndex(若安装了统计工具箱)
ari = rand_index(idx, idx_hc, 'adjusted');
disp(['Adjusted Rand Index between KMeans and HC: ', num2str(ari)]);(如果你没有 rand_index 函数,可以通过自定义或使用其他工具箱函数替代)
4.5 方法总结与应用建议
| 特征 | 层次聚类 | K‑Means |
|---|---|---|
| 是否需预设簇数 | 否,可后期裁剪 | 是,需事先指定 KK |
| 是否稳定(无初始化影响) | 是,完全确定性 | 否,易受初始质心影响 |
| 是否适合不规则形状 | 适中(依赖距离定义) | 否,适用于近球形簇 |
| 是否支持层级可视化 | 是,树状图反映多尺度结构 | 否 |
| 算法复杂度 | O(n2)\mathcal{O}(n^2),不适用于大样本 | O(nkd)\mathcal{O}(nkd),适合大规模数据集 |
层次聚类非常适合用于:
- 探索多尺度生态功能区划;
- 分析群落谱系或时序物种演替关系;
- 地质、环境、组学等需要解释“亲缘性”或“嵌套关系”的问题。
小结与过渡
本节展示了如何利用 MATLAB 实现层次聚类,构建树状图并进行不同尺度的簇划分。与 K‑Means 相比,层次方法不依赖随机初始化、具备良好的可解释性和多分辨率结构表征能力,适用于小中型生态与观测数据集的聚类分析。
下一节将进入 Part III – 密度、概率与谱聚类方法,介绍如何处理非凸形簇、噪声样本或复杂拓扑结构,并结合 MATLAB 中的 DBSCAN 与 GMM 实例展开说明。
