这一节将结合你前面已经标准化并剔除异常值的数据,展示如何在 MATLAB 中实施 K‑Means 聚类,并进行可视化与评价。
3. Part I – K‑Means 聚类分析
K‑Means 是最常用的划分式聚类方法,其基本思想是:在样本空间中设定 KK 个初始质心,然后通过迭代将每个样本划归其最近的质心,更新质心位置,直至结果收敛。K‑Means 假设簇为凸形、均方差相近,因此对高斯分布簇具有良好效果。
3.1 算法调用与参数设置
% 输入变量:标准化后且剔除异常值的特征矩阵
X = X_filtered;
% 聚类数K的设定(可先经验设为3)
K = 3;
% 运行K-Means(推荐使用 'plus' 初始化、多个重复迭代提高稳定性)
opts = statset('Display', 'final');
[idx, C, sumd] = kmeans(X, K, ...
'Distance', 'sqeuclidean', ...
'Replicates', 20, ...
'Start', 'plus', ...
'Options', opts);idx:每个样本所属簇编号(1~K)C:每个簇的中心(质心)坐标sumd:每个簇内平方和误差(SSE)
第 1 次重复,4 次迭代,总距离 = 114.639。 第 2 次重复,9 次迭代,总距离 = 114.639。 第 3 次重复,4 次迭代,总距离 = 114.639。 第 4 次重复,2 次迭代,总距离 = 114.639。 第 5 次重复,6 次迭代,总距离 = 114.639。 第 6 次重复,3 次迭代,总距离 = 114.639。 第 7 次重复,12 次迭代,总距离 = 114.639。 第 8 次重复,14 次迭代,总距离 = 114.639。 第 9 次重复,2 次迭代,总距离 = 114.639。 第 10 次重复,2 次迭代,总距离 = 114.639。 第 11 次重复,3 次迭代,总距离 = 114.639。 第 12 次重复,3 次迭代,总距离 = 114.639。 第 13 次重复,2 次迭代,总距离 = 114.639。 第 14 次重复,2 次迭代,总距离 = 114.639。 第 15 次重复,2 次迭代,总距离 = 114.639。 第 16 次重复,3 次迭代,总距离 = 114.639。 第 17 次重复,16 次迭代,总距离 = 114.639。 第 18 次重复,2 次迭代,总距离 = 114.639。 第 19 次重复,3 次迭代,总距离 = 114.639。 第 20 次重复,2 次迭代,总距离 = 114.639。 距离的最佳总和 = 114.639
3.2 可视化聚类结果(二维)
如数据已降维为 2D(如 PCA),可直接绘图:
% 此处使用 PCA score 中前两主成分
[~, score] = pca(X);
figure;
gscatter(score(:,1), score(:,2), idx, 'rgb', 'o', 6);
xlabel('PC1'); ylabel('PC2');
title('K-Means聚类结果(投影至前两主成分)');
grid on;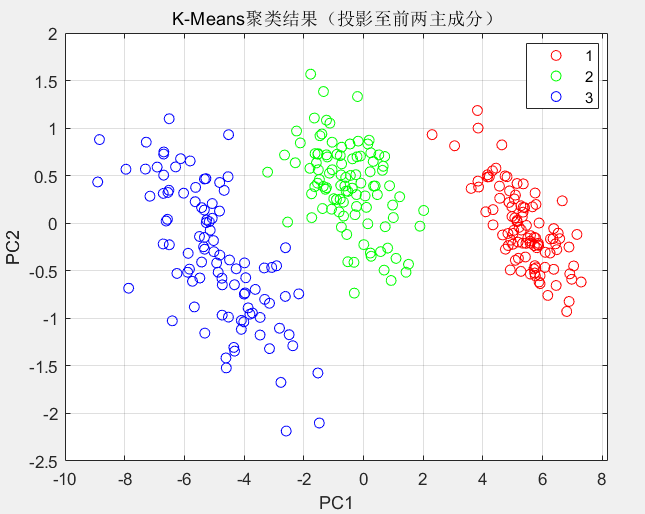
若未降维,可选择任意两维进行可视化:
figure;
gscatter(X(:,1), X(:,2), idx, 'rgb', 'o', 6);
xlabel('SST (标准化)'); ylabel('Salinity (标准化)');
title('K-Means聚类结果示意');
grid on;3.3 评价聚类效果:肘部法则与轮廓系数
① 肘部法则(SSE vs. K)
% 计算不同K值下的总误差平方和
K_range = 2:8;
SSE = zeros(size(K_range));
for i = 1:length(K_range)
[~, ~, sumd_tmp] = kmeans(X, K_range(i), ...
'Distance', 'sqeuclidean', ...
'Replicates', 10, ...
'Start', 'plus');
SSE(i) = sum(sumd_tmp);
end
figure;
plot(K_range, SSE, '-o');
xlabel('聚类数 K');
ylabel('总平方误差 SSE');
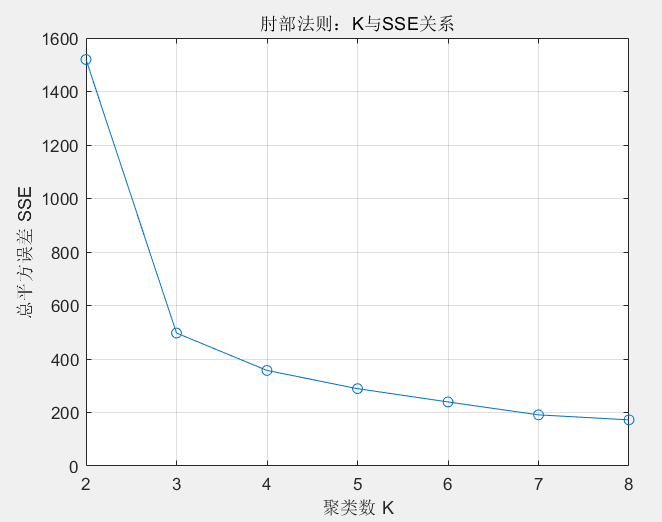
title('肘部法则:K与SSE关系');
grid on;拐点即为推荐的最优 K 值,通常落在 SSE 降速变缓处。
② 平均轮廓系数(Silhouette)
% 使用当前 K 值绘制轮廓图
figure;
silhouette(X, idx, 'sqeuclidean');
title(['K = ' num2str(K) ' 聚类的轮廓图']);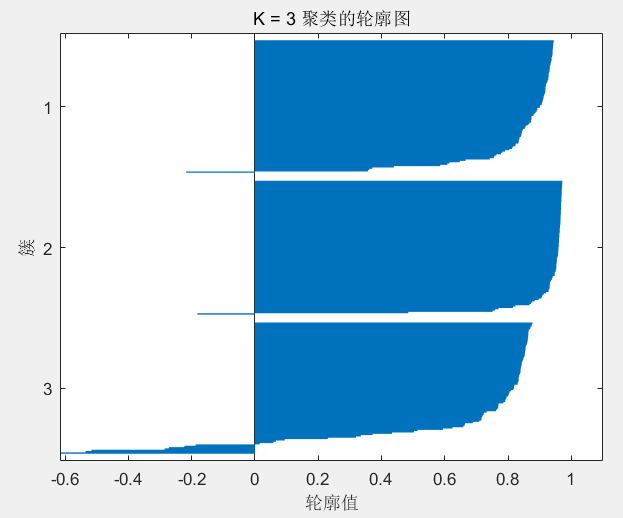
轮廓系数取值范围为 [−1,1][-1, 1],越接近 1 表示簇内一致性好、簇间区分明显。若多数样本 silhouette 值 < 0,说明当前簇划分不合适。
3.4 聚类结果解释与返回整合
可将聚类结果与原始数据合并,便于后续统计分析与图形绘制:
T_result = T_filtered;
T_result.Cluster = idx;
% 只对数值列执行分组统计(排除字符串或分类变量)
% 手动选择数值型列
numericVars = {'SST', 'Salinity', 'Chl_a'};
% 提取数值列子表
T_numeric = T_result(:, [numericVars, {'Cluster'}]);
% 使用 grpstats 分组统计
stats = grpstats(T_numeric, 'Cluster', {'mean', 'std'});
disp(stats);Cluster GroupCount mean_SST std_SST mean_Salinity std_Salinity mean_Chl_a std_Chl_a _______ __________ ________ _______ _____________ ____________ __________ _________ 1 1 100 12.084 1.0471 33.457 0.41433 1.3744 0.27819 2 2 101 17.864 0.96036 34.509 0.28554 0.71539 0.21713 3 3 99 8.0138 1.5933 31.788 0.48217 2.42 0.46745
小结与下一步预告
本节完成了基于标准化海洋生态观测数据的 K‑Means 聚类分析,核心步骤包括:
- 聚类模型拟合与参数优化;
- 可视化结果呈现(主成分空间或特征空间);
- 聚类结构质量评估(SSE 与 silhouette);
- 聚类结果与数据整合用于后续统计检验。
在实际应用中,如发现 K‑Means 无法有效区分非凸形簇或处理离群样本,则应考虑密度或概率模型方法。下一节我们将转入 Part II – 层次聚类(Hierarchical Clustering),介绍如何利用树状图构建多尺度结构,并解释其在空间结构分析与生态谱系推断中的应用。
